[Algorithm] 백준 2468 안전 영역 | BFS, DFS (파이썬)

문제를 정말 오래 풀이하다가 방법이 떠오르지 않아서 풀이를 보고 말았다. 그런데 이전부터 완전히 체득하지 못했던 탐색 알고리즘으로 푸는 문제였다. 이 기회에 BFS와 DFS를 확실하게 이해하고 넘어가기로 했다! 가보자!!

 

 

📝 백준 2468 안전 영역

(개인적으로 문제 번호가 너무 마음에 든다.. 2468이라니 완벽하다..)

https://www.acmicpc.net/problem/2468

n x n의 2차원 배열로 주어지는 지역이 있다. 비가 내려서 특정 높이 이하의 지역이 모두 물에 잠긴다면, 남은 지역에서 서로 인접한(상하좌우) 영역들 중 잠기지 않은 안전 영역의 개수를 구하는 문제다. 대각선으로 붙은 지역은 인접하지 않는 걸로 본다. 높이는 최대 100까지의 자연수이다.

 

🔖 문제 풀이 접근

먼저 비의 높이를 0부터 최대 높이까지 바꿔가면서, 각 높이에서의 안전 영역의 수를 세어 그중 최댓값을 출력한다. 그럼 각각의 높이에서 안전 영역을 찾는 방법은? 처음에는 탐색 알고리즘을 떠올리지 못하고 Union-Find로 풀어야 하나 고민했다. 하지만 그렇게 하면 매번 Union 된 값을 가진 자료를 매번 바꿔야 하는 비효율적인 일이 따라올 것이다..

 

 

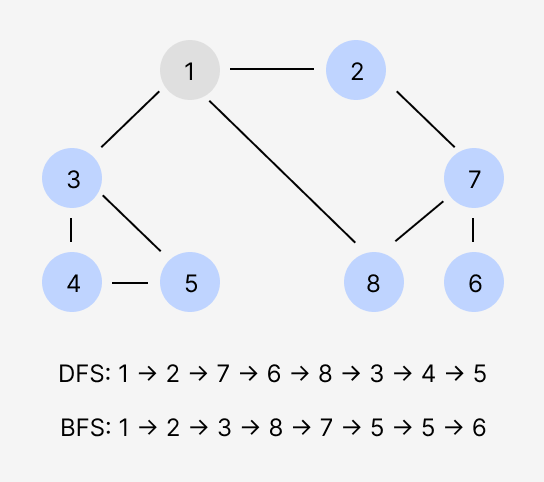
그래서 효율적인 탐색 알고리즘으로 접근해보자. 두 가지 방법이 있다. BFS와 DFS. BFS는 너비 우선 탐색으로 Queue 자료구조를 활용한다. 이름처럼 그래프를 시각적으로 봤을 때, 밑으로 내려가는 것이 아닌 옆으로 먼저 탐색하는 방법이다. DFS는 깊이 우선 탐색으로 Stack 자료구조를 활용한다. 그래프를 시각적으로 봤을 때, 갈 수 있는 가장 아래 노드까지 갔다가 올라오는 방법이다.

 

이 문제에서 탐색 알고리즘을 먼저 떠올리지 못한 이유는 아마도.. 2차원 배열에서 각각의 값들의 인접한 영역이라는 말을 그래프로 해석하지 못했기 때문인 것 같다. 각 칸의 상하좌우(여기서는 대각선은 포함하지 않는다)를 연결된 노드라고 생각한다면 바로 탐색 알고리즘을 적용하는 이유를 이해할 수 있을 것 같다.

 

🔖 문제 풀이 - BFS

🚨 글을 다 쓰고 알았다. 백준의 입력 예시 1번과 글의 예시 값에 다른 부분이 있다. 풀이 이해에는 문제가 없으니 넘어가자!

 

그럼 BFS로 문제를 풀어보자. 풀이 방법을 대략 이해하기 위해 높이가 3일 때 과정을 쭉 살펴보자.

 

 

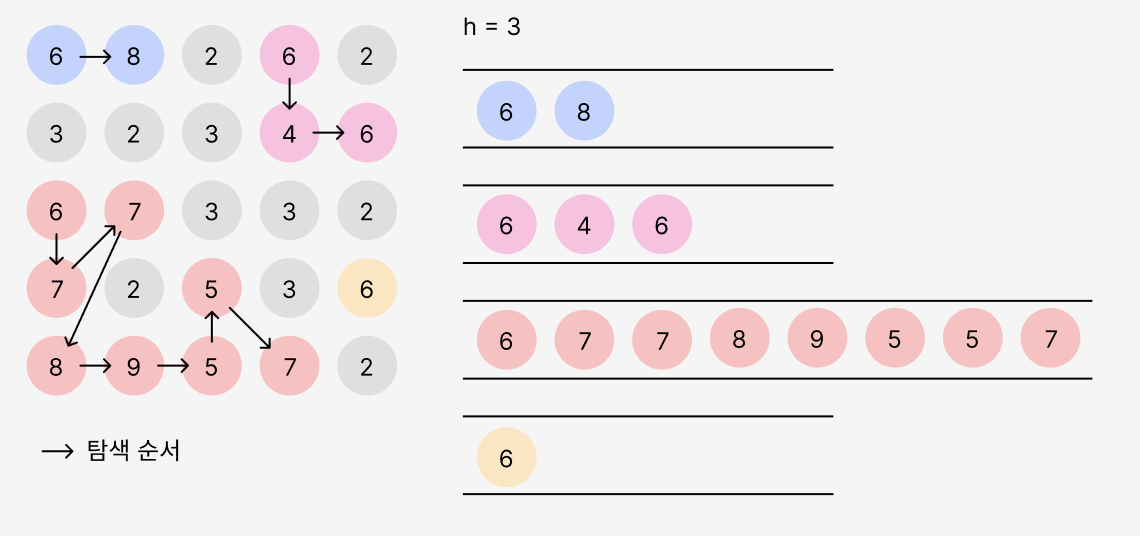
step1. 6 - 8

가장 먼저 (0, 0)에 해당하는 (즉, graph[0][0]) 6을 queue에 넣는다. 그리고 6을 빼고 6과 인접한 상하좌우 노드를 queue에 넣는다. 이 과정에서는 8만 queue에 들어간다. 그리고 8을 뺀다. 더 이상 인접한 값이 없으므로 count를 하나 증가한다.

 

step2. 6 - 4 - 6

(0, 1)에 해당하는 graph[0][1]은 이미 방문했으므로 넘어간다. (0, 2)에 해당하는 graph[0][2]는 침수되었으므로 넘어간다. (0, 3)에 해당하는 graph[0][3]인 6을 queue에 넣는다. 그다음 step1과 동일한 방식으로 6과 인접한 4가 들어간다. 그다음 6이 들어가고 나온다. 더 이상 인접한 값이 없으므로 count를 하나 증가한다.

 

step3. 6 - 7 - 7 - 8 - 9 - 5 - 5 - 7

graph[1]까지는 모두 방문했거나 침수된 값이므로 (2, 0)인 graph[2][0]을 방문하고 queue에 넣는다. 6을 빼고 6과 인접한 값들을 queue에 넣는다. 여기서 순서는 상하좌우이므로 아래 7, 오른쪽 7이 순서대로 queue에 들어간다. 아래 7을 먼저 빼고, 인접한 8을 queue에 넣는다. 들어가 있던 오른쪽 7을 빼고, 인접한 값이 없으므로 넘어간다. 8을 빼고 9를 넣는다. 9를 빼고, 5를 넣는다. 5를 빼고 위쪽 5와 오른쪽 7을 넣는다. 남은 값들을 뺀다. 더 이상 인접한 값이 없으므로 count를 하나 증가한다.

 

step4. 혼자 있는 6도 챙겨준다. 더 이상 인접한 값이 없으므로 count를 하나 증가한다.

 

 

🔖 파이썬 코드 - BFS

이 과정을 그대로 파이썬 코드로 옮겨보자. 최대 높이까지 모든 높이를 반복하고, 모든 배열의 값들을 지나가면서 방문하지 않았고, 침수되지 않는 값들을 탐색한다.

from collections import deque

n = int(input())
graph = [list(map(int, input().split())) for _ in range(n)]

max_height = max(map(max, graph))  # 최대 높이
max_region = 0  # 최대 안전 구역 수

# 상하좌우
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]


def bfs(x, y, visited, height):
    queue = deque()
    visited[x][y] = True
    queue.append((x, y))  # queue에 방문할 노드 추가

    while queue:
        cx, cy = queue.popleft()

        for i in range(4):
            nx, ny = cx + dx[i], cy + dy[i]
            if 0 <= nx < n and 0 <= ny < n:  # 배열 안에 존재하는 값만
            	# 방문하지 않았고, 침수된 높이보다 큰 경우에만 방문
                if visited[nx][ny] == False and graph[nx][ny] > height:
                    visited[nx][ny] = True
                    queue.append((nx, ny))


# 0부터 가장 높은 높이까지 방문
for h in range(max_height + 1):
    visited = [[False] * n for _ in range(n)]
    count = 0

    for i in range(n):
        for j in range(n):
            if visited[i][j] == False and graph[i][j] > h:
                bfs(i, j, visited, h)
                count += 1  # 탐색이 끝나고 인접한 곳이 없으면 증가

    max_region = max(max_region, count)

print(max_region)

 

🔖 시간 복잡도 - BFS

1. 최대 높이까지 반복한다. (최대 100회)

2. 각 높이마다 graph의 모든 값을 확인한다. 이차원 배열이므로 O(n^2)

3. bfs로 각 값들은 한 번씩만 방문한다.

최종, O(h x n^2)이고, 최대 100 x 100 x 100 = 1,000,000으로 1초 안에 넉넉하게 통과할 수 있다.

 

 

💡 문제 풀이 - DFS

이렇게 똑같은 과정을 단순히 탐색만 DFS로 진행할 수 있다. BFS 코드에서 bfs 함수를 사용하는 부분만 dfs로 변경하면 된다. DFS는 다만 재귀를 사용하기 때문에 안정성을 고려하면 BFS를 더 추천한다. 하지만 시간 복잡도는 동일하기 때문에 뭐.. 큰 차이는 없다고 한다! 풀이 자체는 DFS가 좀 더 이해하기 쉬울 수도 있다. 한번 해보자.

 

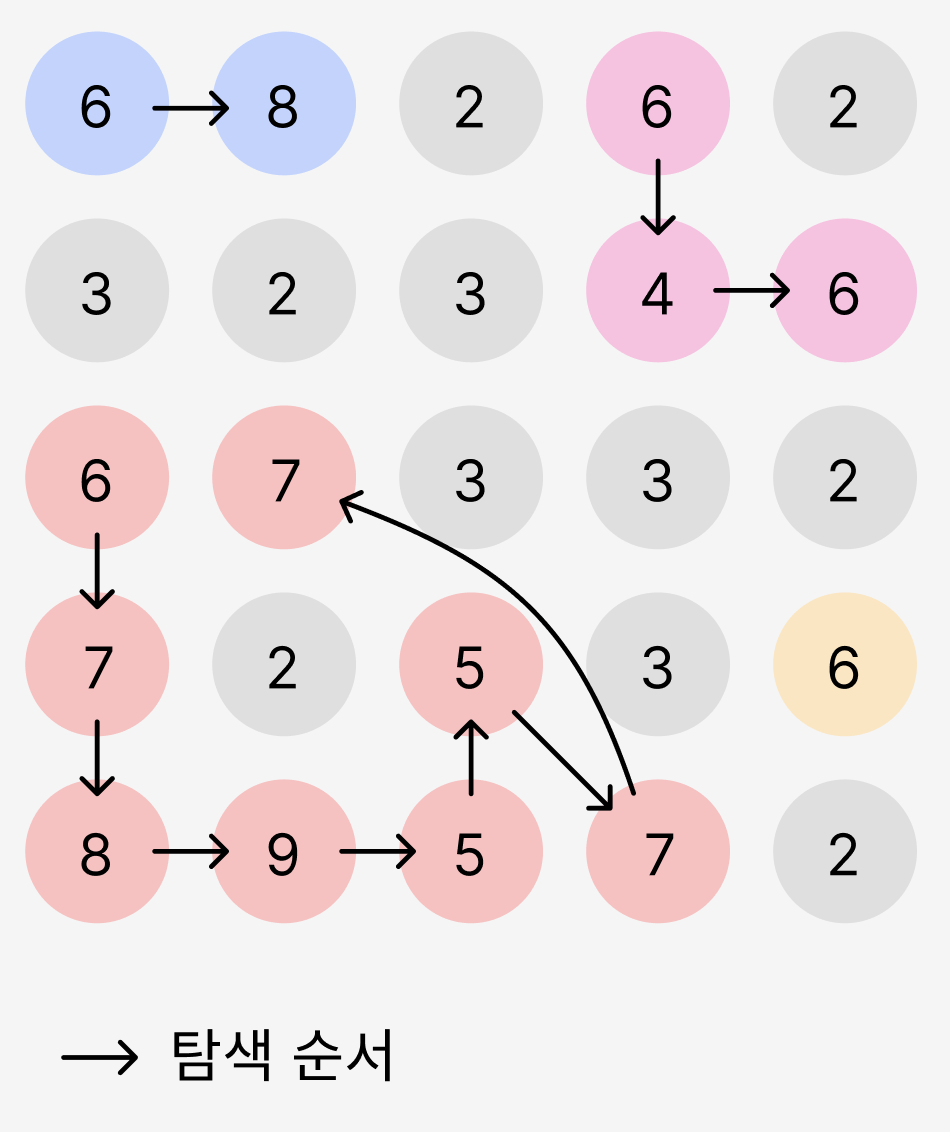
파랑, 분홍, 노랑 영역은 생략하고, 빨강 영역만 살펴보자. 먼저 (2, 0)인 6으로 시작한다. 그다음 상하좌우 순서이므로 아래쪽 7을 먼저 방문한다. 방문한 값에서 또 인접한 영역을 먼저 살피게 되므로, 아래쪽 8을 탐색한다. 순차적으로 9, 5를 방문한다. (4, 2)인 5에서 위쪽 5를 먼저 방문하고, 위쪽 5는 인접한 값이 없으므로 오른쪽 7을 방문한다. 그리고 잊지 말고 처음 6이 인접했던 (2, 1)인 7을 방문하고 끝낸다.

 

 

💡 파이썬 코드 - DFS

이 과정에서 dfs를 파이썬 코드로 옮겨보자. 상하좌우를 보면서 먼저 보게 되는 값의 상하좌우를 또 탐색하고 탐색하며 재귀적으로 풀어내면 된다.

import sys
sys.setrecursionlimit(1000000)  # 재귀를 사용하게 되므로, 제한을 풀어줘야 한다!

def dfs(x, y, height, visited, graph, n):
    print(h, x, y, graph[x][y])
    visited[x][y] = True

    for d in range(4):
        nx = x + dx[d]
        ny = y + dy[d]

        if 0 <= nx < n and 0 <= ny < n:
            if not visited[nx][ny] and graph[nx][ny] > height:
                dfs(nx, ny, height, visited, graph, n)

 

💡 시간 복잡도 - DFS

시간 복잡도는 BFS와 동일하다. 탐색하는 과정만 다를 뿐, DFS 또한 각 값들을 한 번씩만 방문하기 때문에 O(h x n^2)이 된다.

 

 

🍀 마무리

이 문제를 접하고 가장 먼저 떠오른 풀이 방법은 유니온 파인드였다. 인접한 영역끼리 친구를 맺어주고, 그 수를 찾으려고 했었다. 하지만 풀이를 막상 하려니 방법이 떠오르지 않았다. 나중에 이 방법으로 풀어도 되냐고 GPT에게 물어봤더니 비의 높이에 따라 연결 상태가 바뀌기 때문에 고정된 연결 관계를 저장하는 유니온 파인드와는 어울리지 않는다고 했다. 매 시뮬레이션마다 새로운 연결 상태를 파악하기 위해 DFS/BFS가 더 적합하다고.

 

덕분에 그래프 탐색 유형 중 DFS/BFS를 확실히 이해하고 넘어갈 수 있었다. 이전에는 연결된 노드가 담긴 그래프를 탐색하는 걸로만 생각하고 풀이 방법을 떠올리지 못했던 것 같다. 휴우 이번 문제를 풀고, 이해하고, 글을 작성하는데 시간을 꽤 썼지만, 그동안 묵혀두었던 짐을 하나 푼 기분이다. 아싸.